Influence of rotation

To study the influence of the rotation, we first look for Lagrangian points. The latter are found by setting the right terms of equations (6) to zero. Substituting $p_x$, $p_y$ and $p_z$, the Lagrangian points are solutions of the following equations :

$$\partial_x\Phi_w = \Omega_p^2 x,$$

$$\partial_y\Phi_w = \Omega_p^2 y,$$ (9)

$$\partial_z\Phi_w = 0.$$

With the form (3) of the warped potential, one can easily see that the $z$ coordinate must satisfy :

$$z = \Delta z,$$ (10)

with $\Delta z$ defined in equation (2). This causes the two first equations of (10) to become :

$$\partial_x\Phi_0 = \Omega_p^2 x,$$ (11)

$$\partial_y\Phi_0 = \Omega_p^2 y,$$

which corresponds to the definition of the corotation, where $\Phi_0$ is the potential without perturbation (Eq. (1)). Thus the Lagrangian points are degenerated, forming an annulus following the density maximum with a projection on the $z=0$ plane corresponding to the corotation without perturbation ($w=0$).

Despite the fact that a direct and retrograde rotations respectively add and remove resonances, the type of bifurcations as well as the stability and the shape of orbits are not affected by a global pattern speed. This has been tested in the range $-30 > R_c$ and $R_c > 30\,\textrm{kpc}$, where $R_c$ is the corotation radius and a negative value corresponds to a retrograde rotation.

For a radius less than $40 \textrm{kpc}$, both prograde and retrograde 1:1 resonances are not observable in this range of pattern speed. For a corotation of $7\,\textrm{kpc}$ they appear only beyond $40\,\textrm{kpc}$ (resp. $30\,\textrm{kpc}$). Thus they have not been studied.

The main influence appears when we look at the consistency of orbits with the mass density. If the warp is mostly self-gravitating and made of thin and distinct tube orbits, one can check the self-consistency constraint by noting that the spatial occupation of a periodic orbit is locally inversely proportional to its local speed ( $t_{so} \sim 1/\vert v\vert$). The reason is explained by the fact that at a given point of the orbit, the local speed remains constant in time. This argument is not available at exceptional points, for example the points where an orbit crosses itself. Since the density is proportional to the spatial occupation time, it must also be proportional to the inverse speed along the orbit ( $\rho \sim t_{so}\sim 1/\vert v\vert$). Strictly this condition is only fulfilled by a structure entirely made of distinct exactly periodic orbits, such as a disk made of circular orbits. Nevertheless the check is useful in this problem because few hot orbits far from periodic round orbits are expected to exist.

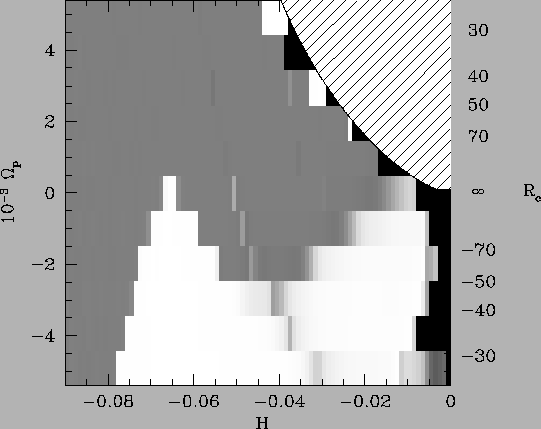
In practice, the consistency has been calculated using the indice $I$ defined by the norm :

$$I(\Omega_p,H)=\frac{1}{2\pi}\left[\int_0^{2\pi}\left[\Delta\rho(\phi)- \Delta u(\phi)\right]^2d\phi\right]^{1/2},$$ (12)

with

$$\Delta\rho(\phi)=\frac{\rho(\phi)-\rho_{min}}{\rho_{max}-\rho_{min}},$$ (13)

$$\Delta u(\phi)=\frac{u(\phi)-u_{min}}{u_{max}-u_{min}},$$ (14)

and $u(\phi)=1/\vert v(\phi)\vert$. The values $\rho_{min}$, $\rho_{max}$, $u_{min}$ and $u_{max}$ are calculated over a period of the azimuthal angle $\phi$. When $\Delta\rho$ and $\Delta u$ vary in the same direction, $I=0$ and the orbit is consistent. If they vary inversely, as two cosines with a phase difference of $\pi$, $I=\sqrt{\pi}/{2\pi}$.

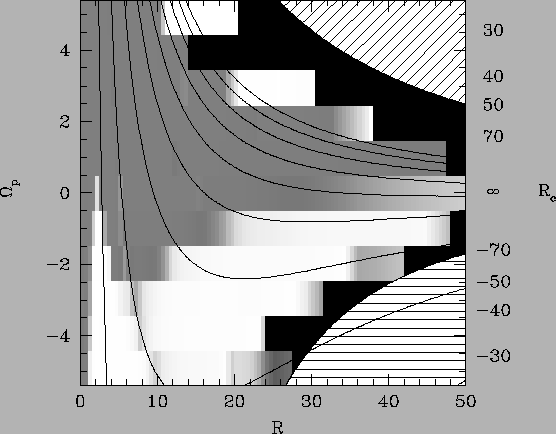
We have tested the consistency of families pk with respect to the energy (Fig. 11) and radius (Fig. 12), which is more convenient in galactic dynamics. This as been calculated for different (direct and retrograde) pattern speeds between $-30 > R_c$ and $R_c > 30\,\textrm{kpc}$ corresponding to $-4.5\cdot10^{-3} < \Omega_p < 4.5\cdot10^{-3}\,\textrm{Myr}^{-1}$. The white regions correspond to $I=0$ (consistency) while the darker gray correspond to a value of $\sqrt{\pi}/{2\pi}$ (inconsistency). The shaded parts give the limit of the computation, either because of the corotation or because of the positive energy regions. The black pattern points out the missing data due to computational difficulty arising because of the proximity of the forbidden regions.

Figure 11: Consistency of orbit occupation with the mass density as a function of the energy and the global rotation. The dark gray corresponds to inconsistent regions while the white are consistent regions. The black parts are missing data. The shading part represents the limit of the corotation.

Figure 12: Same graph than in Fig. 11 but as a function of radius $R$. The upper shading part represents the limit of the corotation. While the lower is the region where $H>0$. The vertical resonances ( $\nu = k\, \Omega$, $k=2,\ldots 10$) are drawn in solid lines.

For a direct rotation, except in small regions near the corotation, the inverse local speed along an orbit varyies exactly in opposition to the density ( $I=\sqrt{\pi}/{2\pi}$). This causes it to depopulate the higher density regions to the advantage of the lower. The density distribution is also slowly modified. However, for a slowly retrograde rotation a zone appears around $3\,\textrm{kpc}$, where the inverse local speed varies exactly as the density. This latter is also reinforced and the potential is self-consistent. This zone grows with increasing rotation and a second zone appears for larger radii. For a corotation smaller than $R_c=-50\,\textrm{kpc}$ the zones of consistency cover the whole disk under the curve of zero energy.

The same work applied to the subfamilies $sk\pm$ reveals that they are clearly inconsistent with the density distribution, but these families are also less relevant with the assumption of almost circular rotation.