Next: Surfaces of section around
Up: Families of periodic orbits
Previous: Families without perturbation
The break in the  symmetry transforms the family of circular orbits in the unperturbed
model into a set of families
symmetry transforms the family of circular orbits in the unperturbed
model into a set of families 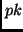 (main families) with
(main families) with 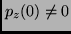 .
The significance of the indice
.
The significance of the indice 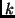 will be explained
further.
Except at bifurcations, the
will be explained
further.
Except at bifurcations, the 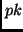 families are stable.
families are stable.
The shape of the corresponding orbits can be approximated
with the following parametric function:
parametrised by the azimuthal angle 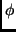 . For increasing
. For increasing 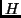 ,
, 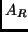 increases from
0 to
increases from
0 to  kpc, while
kpc, while 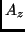 increases from 0 to
increases from 0 to 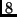 kpc.
This latter variation corresponds
almost exactly to the amplitude of the warp as a function of radius
(
kpc.
This latter variation corresponds
almost exactly to the amplitude of the warp as a function of radius
(
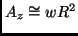 ). In other words, the main orbit family follows
the density maximum at any radius.
). In other words, the main orbit family follows
the density maximum at any radius.
Another influence of the warp is to move the bifurcations
toward slightly lower energies. The corresponding transverse bifurcations
arise at 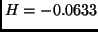 ,
, 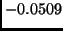 ,
, 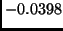 ,
, 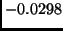 , and
, and 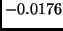 .
Moreover, a new bifurcation takes place within the limits of the diagram at
.
Moreover, a new bifurcation takes place within the limits of the diagram at 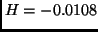 ,
where the subfamily starting at
,
where the subfamily starting at 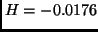 rejoins the main family. The other
families would also rejoin the main family at higher energies, yet they would reach
radii larger than
rejoins the main family. The other
families would also rejoin the main family at higher energies, yet they would reach
radii larger than
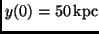 , which was chosen as a limit for our study of a
warped disk.
, which was chosen as a limit for our study of a
warped disk.
Figure 3:
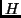 -
-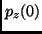 phase space (
phase space ( ).
).
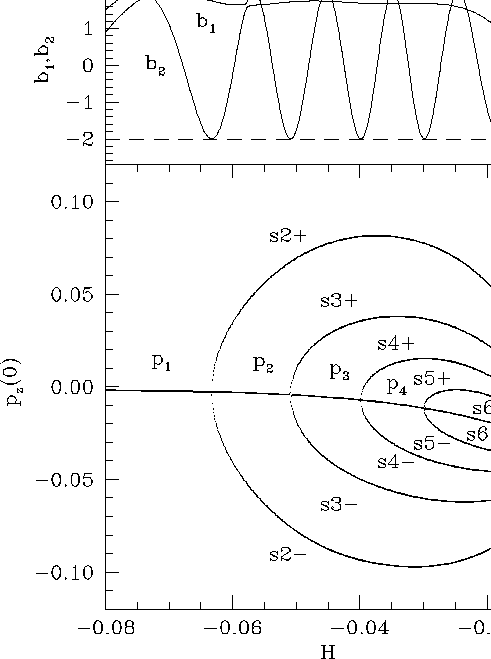 |
The subfamilies coming from
the corresponding transverse bifurcations are given the symbol
``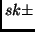 '' where
'' where 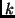 gives the frequency
ratio
gives the frequency
ratio 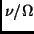 at the corresponding bifurcation and the sign is the
one of the difference of
at the corresponding bifurcation and the sign is the
one of the difference of 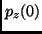 between the subfamily and the main family.
These families evolve in the same way as family
between the subfamily and the main family.
These families evolve in the same way as family 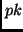 , i.e. they follow the warped
disk, so may be significantly populated in a real disk. Note
that the families with an odd
, i.e. they follow the warped
disk, so may be significantly populated in a real disk. Note
that the families with an odd 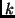 conserve the bi-symmetry of the potential, which is not the
case when
conserve the bi-symmetry of the potential, which is not the
case when 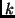 is even.
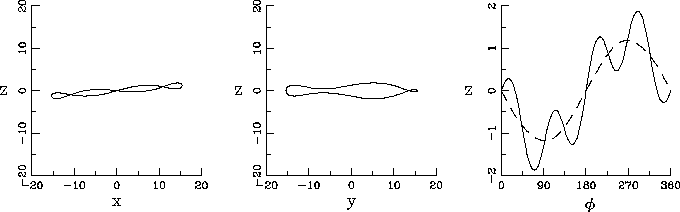
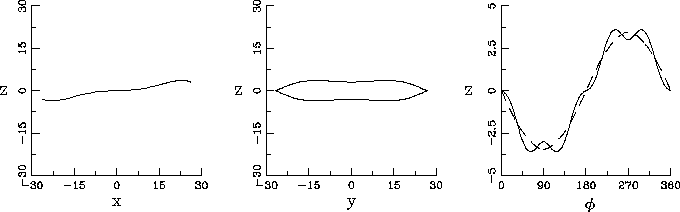
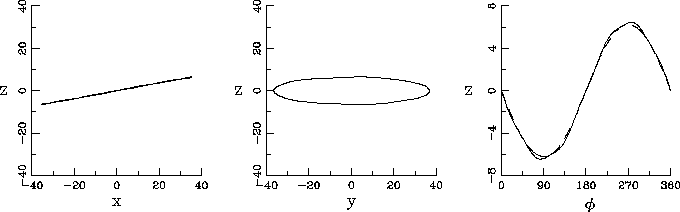
Fig. 4 displays a set of three orbits extracted from different subfamilies,
is even.
Fig. 4 displays a set of three orbits extracted from different subfamilies,
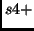 ,
, 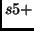 and
and 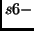 . The right panels show the elevation
. The right panels show the elevation 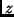 of the orbits as a function
of the azimuth
of the orbits as a function
of the azimuth 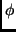 in comparison to the elevation of the corresponding main family
(dashed lines). The more the energy grows, the more the subfamilies follow well the main
orbit.
in comparison to the elevation of the corresponding main family
(dashed lines). The more the energy grows, the more the subfamilies follow well the main
orbit.
Figure 4:
Projections over the 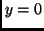 ,
, 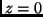 planes and
the evolution of
planes and
the evolution of 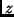 as a function of azimuthal angle
as a function of azimuthal angle 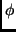 of orbits
of the families
of orbits
of the families 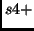 (
(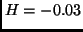 ),
), 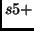 (
(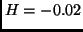 ) and
) and 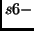 (
(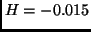 ).
The dashed line represents the
potential minimum of the warped disk at a fixed radius which is similar to the main
family.
).
The dashed line represents the
potential minimum of the warped disk at a fixed radius which is similar to the main
family.
|
|
Although in the absence of the warp all subfamilies are stable, this is no longer the case
with a weak warp. This point will be discussed further below.



Next: Surfaces of section around
Up: Families of periodic orbits
Previous: Families without perturbation
2002-03-16
![]() symmetry transforms the family of circular orbits in the unperturbed
model into a set of families
symmetry transforms the family of circular orbits in the unperturbed
model into a set of families ![]() (main families) with
(main families) with ![]() .
The significance of the indice
.
The significance of the indice ![]() will be explained
further.
Except at bifurcations, the
will be explained
further.
Except at bifurcations, the ![]() families are stable.
families are stable.
![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
Moreover, a new bifurcation takes place within the limits of the diagram at
.
Moreover, a new bifurcation takes place within the limits of the diagram at ![]() ,
where the subfamily starting at
,
where the subfamily starting at ![]() rejoins the main family. The other
families would also rejoin the main family at higher energies, yet they would reach
radii larger than
rejoins the main family. The other
families would also rejoin the main family at higher energies, yet they would reach
radii larger than
![]() , which was chosen as a limit for our study of a
warped disk.
, which was chosen as a limit for our study of a
warped disk.